7.4. Initializing Arrays

Time: 00:03:33 | Download: Large, Large (CC), Small | Streaming, Streaming (CC) | Slides (PDF)

Whenever a program creates a new array, automatically or dynamically, the elements initially contain unspecified values. Memory can never be empty, but until the program explicitly stores a value in an array element, we say the value is "unknown," "unspecified," or "undefined;" colloquially, we say it contains "garbage." Often, the program initializes the elements one at a time with user or file input. However, programmers can initialize the array elements efficiently and compactly with an initializer list when they know the initial values at compile time. Figure 1 illustrates the initialization syntax and its most recent evolution.

int test[5] = { 0, 1, 2, 3, 4 };
 
int* test = new int[5];
(a)(b)
int test[5]{ 0, 1, 2, 3, 4 };
 
int* test = new int[5]{ 0, 1, 2, 3, 4 };
(c)(d)
Compile-time array initialization. The initial element values form a comma-separated list enclosed between a pair of braces. The program processes the initializer list in English reading order - from left to right. It saves the first value in element 0, the second value in element 1, and so on until it saves the last value in the last element. The number of values in the initializer list must be less than or equal to the size of the array. If the array is longer than the initializer list, the program initializes the excess elements to 0.
  1. Initializing an automatic array. This syntax dates back to the C programming language
  2. The C++ syntax didn't support dynamic array initialization before the adoption of the 2015 ANSI standard en bloc
  3. The ANSI 2015 standard permits a slightly simplified syntax, similar to Java's, for initializing automatic arrays
  4. The ANSI 2019 standard now supports the initialization of dynamic arrays using a syntax nearly identical to Java's

The number of values in the initializer list may never exceed the number of elements in the array. But it's okay if the array is larger than the number of initializer values. When more elements are in the array than values in the initializer list, the computer automatically initializes the remaining or unmatched elements to zero. This behavior suggests a compact notation or "trick" for initializing all array element values to zero.

int test[5] = {}; or int test[5]{};
 
int* test = new int[5]{};
(a)(b)
Zeroing array elements. An empty initializer list is a compact notation for initializing all list elements to zero.
  1. Setting all elements of an automatic array to 0
  2. Setting all elements of a dynamic array to 0

Specifying the size of an array but using an empty initializer list is only one useful "trick." Another notation allows us to omit the size of the array but to specify the size implicitly with the number of elements in the initializer list. This notation, more limited in use than the element zeroing notation, is only useful when programmers know the element values in advance - for example when an array supports a repetitive computation.

int month_length[12] =
{
	31, 28, 31, 30,
	31, 30, 31, 31,
	30, 31, 30, 31
};
 
int month_length[] =
{
	31, 28, 31, 30,
	31, 30, 31, 31,
	30, 31, 30, 31
};
(a)(b)
Array initialization: Days per month example. The two code fragments illustrate a typical situation where a programmer knows the array element values at compile time. Except for February, the number of days per month is fixed and, therefore, known at compile time (the value for February can be updated as needed after the array is created and initialized).
  1. The first array definition contains redundant information: it specifies the array's size. First, it specifies the size with the value inside the brackets: [12]. Next, it implies the size with the number of elements in the initializer list.
  2. To create an array with the same number of elements as the number of values in the initializer list, we may omit the array size (but notice that the brackets are still required).

We can extend the notation of Figure 3 to two-dimensional arrays.

int test_scores[5][4] =
{
	95, 98, 97, 96,
	79, 89, 79, 85,
	99, 98, 99, 99,
	90, 89, 83, 86,
	75, 72, 79, 69
};

int test_scores[][4] =
{
	95, 98, 97, 96,
	79, 89, 79, 85,
	99, 98, 99, 99,
	90, 89, 83, 86,
	75, 72, 79, 69
};
(a)(b)
Initializing two-dimensional Arrays. The need for and usefulness of initializing arrays with more than one dimension is much less than for one-dimensional arrays. Nevertheless, C++ permits this in two slightly different ways. In both cases, the program processes the values in the list left to right and stores them in the array elements by rows: 
test_scores[0][0] = 95
test_scores[0][1] = 98
	. . . .
test_scores[1][0] = 79
	. . . .
    The code arranges the values by rows and columns only to make it easier for people to read - writing the statement on a single line is valid.
  1. Programmers can specify both dimension sizes.
  2. The first dimension or row size is redundant and may be omitted. However, programmers may only omit the first size - the second and subsequent sizes are required.

It's possible to extend the notation of Figure 4 to higher dimensions but doing so results in code that is hard to read, understand, and maintain. Fortunately, higher-dimensioned arrays are less common in most problem domains, and the need to initialize multidimensional arrays is even less common. One last bit of notation, also rare, is left to explore.

Calculating An Array's Size

The following notation allows us to write code that counts the number of elements in an array. Its usefulness is generally limited to exceptional cases where the program has a large array of unchanging data similar to (but usually larger than) the month_length array above. Even then, the technique is most useful if the number of elements, and therefore the size of the array, is also subject to change.

int month_length[] =
{
	31, 28, 31, 30,
	31, 30, 31, 31,
	30, 31, 30, 31
};
int number = sizeof(month_length)/sizeof(int);
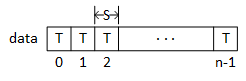
 A picture of an array named data represented as a rectangle. Each array element, represented by a square, is of type T. The element indexes range from 0 to n-1. 
T data[n];
(a)(b)
Counting array elements. The sizeof operator returns the size of its operand in bytes. When the operand is a variable, sizeof returns the total number of bytes allocated to store it. When the operand is a data type, the returned value is the number of bytes needed to store an instance of that type in memory.
  1. An example of using the sizeof operator to calculate the number of elements in an array.
  2. A pseudo-code explanation based on a generalized data type, T
    • Let T be some valid data type
    • Let S be the size in bytes of T, which implies that sizeof(T) = S
    • data is an array of T elements (i.e., each square in the illustration represents one array element of type T)
    • So, sizeof(data) = n × S
    • Therefore, the number of elements in data is sizeof(data) / sizeof(T) = n × S/S = n.
Unfortunately, this technique does not work with arrays passed as function arguments.

Understanding what takes place when we use the sizeof operator will make it easier for us to appreciate when we can use it and when using it is not appropriate.

An array named data represented as a rectangle. The name data names the entire array. 
T data[n];
 Pointing to an array involves two variables. The pointer variable p stores the address of an array created on the heap with the new operator (i.e., points to the array). 
void function(T* p) {...}
or 
T* p = new T[n];
(a)(b)
Understanding sizeof. The illustration continues to use the pseudo-code and the general data type T introduced in the previous figure.
  1. data names the entire array, so sizeof(data) is the total number of bytes allocated to store the array: n × sizeof(T)
  2. C++ always passes arrays to functions by pointer. When applied to a pointer, sizeof returns the size of the pointer variable, not the data to which it points. So, sizeof(p) is the size of the pointer variable, that is, the number of bytes required to store an address (usually 4 or 8 bytes), which is independent of the actual size of the array.