7.10. Stacks And Stack Operations

Time: 00:03:51 | Download: Large, Large (CC), Small | Streaming, Streaming (CC) | Slides (PDF)

A stack is a simple last-in, first-out (LIFO) data structure - the last data element stored on a stack is the first data element retrieved from it. The common analogy is a stack of plates in a cafeteria: when you go through the line, you pop the top plate off of the stack; the dishwasher (stepping away from reality a bit) pushes a single clean plate on top of the stack. So, a stack supports two basic operations: push and pop. Some stacks also provide additional operations: size (the number of data elements currently on the stack) and peek (look at the top element without removing it).

An illustration of a stack as a pile of elements. Programs push new elements on the top of the stack and remove them by popping them off the top.
The primary stack operations. Programs store a new data element by pushing it on the top of the stack. A data element is retrieved by popping the top element off the top of the stack and returning it.

Stacks are important data structures in their own right. Programmers can implement stacks in many ways, including arrays, which we do here as an array example. The bottom of the stack is the first array element (i.e., the element at index location 0). The stack top always changes as elements are pushed on and popped off the stack. So, we'll use a second variable, called a stack pointer, to keep track of the stack top. The stack pointer is an index into the array representing the stack.

A picture of a stack implemented as an open-ended array. We draw the array here so that element 0 is at the bottom, and the indexes increase upward. We also initialize to 0 an integer variable named <kbd>sp</kbd> (for stack pointer), which is where the program puts the first element pushed on the stack.
Implementing a stack as an array. The array is drawn vertically rather than horizontally to better match the typical depiction of a stack, with the beginning of the array at the bottom and the other end left open. The array index numbers are on the left side of the array. Initially, the stack is empty, denoted by setting sp to 0.

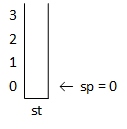
Implementing a stack as an array has two shortcomings. First, the size of the stack (i.e., the maximum number of elements that the stack can hold) must be a compile-time constant. Second, the type of data stored in the stack (i.e., the array type) is specified when the array is defined - when we write the code. We'll strengthen these features as we refine our initial implementation in subsequent chapters, but the final, clean result requires templates in Chapter 13.

The following discussion describes how stacks work generally and as implemented with arrays specifically. So, for now, we "solve" the two problems presented above by simply creating a stack that can only store characters implemented as a char array whose size is left ambiguous (specified as a symbolic constant implemented with macro, enum, or const).

char	st[SIZE];
int	sp = 0;

Stack Behavior

The various stack operations are easy to implement, but notice that push and pop use post-increment and pre-decrement respectively (this is crucial for the algorithm to work).

push
st[sp++] = data (sp must be < SIZE)
pop
return st[--sp] (sp must be > 0)
size
return sp;
peek
return st[sp-1]

Based on these operations, the snapshots shown in Figure 3 illustrate the appearance of a stack as data (characters) are stored in or pushed onto it.

Operation Picture Execution
Stack is empty 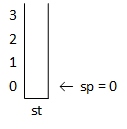The stack pointer, sp, indexes into the array st and logically determines how many elements are on the stack. The stack st is empty, and sp is 0.   
push('A');
 The example pushes the letter 'A' on the stack, storing it at st[0] and incrementing sp to 1. 
st[0] = 'A';
sp = 0 + 1;
 
push('B');
 The example pushes the letter 'B' on the stack, storing it at st[1], and increments sp to 2. 
st[1] = 'B';
sp = 1 + 1;
 
push('C');
 Finally, the example pushes the letter 'C' on the stack, storing it at st[2] and incrementing sp to 3. 
st[2] = 'C';
sp = 2 + 1;
The push operation illustrated. Each call to the push function (left column) pushes a data element onto the stack. The main instruction in the push function is st[sp++] = data, where "data" is the function argument. The middle column abstractly illustrates how the stack (the array and the stack pointer) appears after each call to the push function. The right column breaks the behavior of the push function into two steps.

Similarly, we can retrieve the data (characters) stored on a stack by popping them off and returning them.

Operation Picture Execution 
data = pop();
 The order of operations is significant: the example decrements sp to 2 before using it as an index. After decrementing sp, the example pops the element at st[2], 'C,' off the stack. st[2] still stores a 'C,' but that index location is now logically empty, making it unnecessary to remove the value from the array physically. 
sp = 3 - 1;
return sp[2];
 
data = pop();
 The example decrements sp to 1 and the element at st[1], 'B,' is popped off the stack. 
sp = 2 - 1;
return sp[2];
 
data = pop();
 Finally, the example decrements sp to 0, and the element at sp[0], 'A,' is popped off the stack. Although the letters A, B, and C are still physically in the stack array st, the stack is logically empty because the stack pointer, sp, is 0. 
sp = 1 - 1;
return sp[2];
The pop operation illustrated. Each call to the pop function (middle column) removes a data element from the top of the stack and returns it. The main instruction in the pop function is return st[--sp]. The middle column abstractly illustrates how the stack (the array and the stack pointer) appears after each call to the pop function. The right column breaks the pop function's behavior into two steps. Notice that the pop operations logically remove a character from the stack array - the program treats the slots at and above the stack pointer as empty - but the data remains in the array. So, the next push operation will overwrite the data at the stack pointer. The stack at the bottom of the table is logically empty.

Maintaining a stack as two discrete variables (an array and a stack pointer) is cumbersome, error-prone, and makes it difficult to support multiple stacks in a program. Fortunately, we can solve these problems (if somewhat inelegantly) if we implement a stack as a struct. But even after settling on a structure-based solution, there are still two possible paths that we can take. We base the first implementation on automatic or local variables and the second on dynamic or heap variables. More elegant solutions based on classes and templates will follow in subsequent chapters.