3.1. Basic Flow Of Control

Time: 00:01:27 | Download: Large, Large (CC), Small | Streaming, Streaming (CC) | Slides (PDF)

Imagine that we print out a program on fan-fold paper, the long, continuous paper used by old dot-matrix printers. Further, imagine that we spread the program out on a long table. Find the main function, and place the tip of a marker at the top. Now, mentally run the program while tracing each instruction with the marker as you run it. The marker traces the branches taken by if-statements and coils around the program's loops. We must pick up the marker and move it when we call a function, but we return it to the original trace when the function ends. The trace left in ink on the paper is the flow of control (aka, the nexus of control).

Classifying control statements. Programs written with imperative programming languages consist of a sequence of statements. The computer hardware maintains a counter, automatically advanced each time it processes a statement, indicating the next operation to read and execute. So, the statements execute sequentially or one after another. C++, Java, and other imperative languages generally provide three basic control statements: sequential, branches, and loops. Branches and loops are more complex, internally altering the sequential statement execution. Due to their complexity, programmers often further decompose them into different kinds of loop and branch statements.

Each kind of statement solves a particular programming problem and adds power and complexity to a program. Nesting one statement inside another amplifies the statements' computational power and complexity. C++ does not limit how deeply we can nest flow control statements, but the logic can become difficult to follow if they are too deeply nested. What constitutes "too deeply" is a function of the program and the problem that the program solves, but a good rule of thumb is to limit nesting to four (or, if the code is otherwise simple, five) levels of branches and loops.

Keywords And Symbols

All imperative programming languages build the flow of control statements with keywords and symbols. They often use different words and symbols to represent the same concepts. For example, C, C++, Java, and C# use { and } to delimit a control statement's body. Pascal, Modula II, and Ada use the keywords begin and end for the same purpose. Although not as evident, Python uses indentation to group control statements.

Keywords Symbols
  1. if
  2. else
  3. switch
  4. case
  5. for
  6. while
  7. do
  8. break
  9. continue
  1. (
  2. )
  3. ;
  4. :
  5. { (sometimes optional)
  6. } (sometimes optional)
Control statements keywords and symbols. C++ is a case-sensitive programming language. Case-sensitive means that if we write two words with the same letters but use a different case for even one letter, the compiler interprets them as two distinct words. So, for example, "while" is not the same as "While." C++ spells all keywords used to create flow-of-control statements with all lower-case letters. Furthermore, the control statements require several special symbols, most of which are required.

Sequential Statements

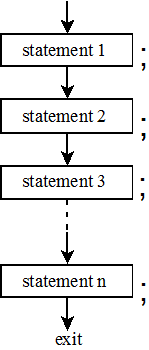
The examples presented in Chapter 2 utilized only sequential statements: statements that execute one after the other in a strict top-to-bottom order. Figure 1 graphically illustrates the behavior of sequential statements.

An illustration of sequential statements where a rectangle represents each statement. Arrows pointing downward from one statement to the next emphasize the sequential order of operation. In essence, they define the flow of control.
Sequential statements. Sequential statements are simple. They run from the top to bottom (i.e., from the first to the last). Each statement ends with a semicolon and runs exactly once.

Although sequential statements are important and powerful, only simple programs complete their tasks without branches and loops. However, before we can look at branches and loops, we must first explore two prerequisite concepts: block structure and logical expressions.