 |
 |
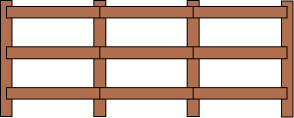 |
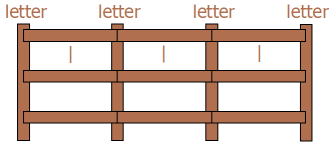
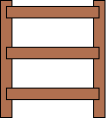
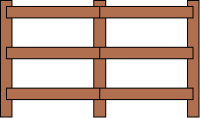
wiktionary.org provides a simple, clear definition of the fence post problem:
If one wants to say "lay a fence post, then a length of fence, then repeat," then a special case must be made for the final fence post. If one wants to say "lay a length of fence, then a fence post, then repeat," then a special case must be made for the initial fence post.
[Downloaded 2019/01/12]