7.8. Index Order

Previously, I stated that when defining a two-dimensional array, the first size is the number of rows, and the second is the number of columns. I'm deliberately using the labels "rows" and "columns" because their meanings are well-established and understood in the context of tables. But does choosing one array index order over the other make a difference? Are we forced to use rows × cols, or can we define it as cols × rows? Again, I'm deliberately using a multiplication notation to make a point: multiplication is commutative, so the product rows × cols is the same as cols × rows, suggesting there is some ambiguity, or, depending on your point of view, some flexibility with the index order.

Array Definitions	Memory Allocation
int array[2][3]; int array[3][2];

Choosing Rows × Columns

Although index order doesn't affect the amount of memory allocated for a two-dimensional array, there are numerous compelling reasons for insisting that the first dimension represents rows and the second columns. So, throughout the text, I maintain that the "correct" index order is rows × cols or array[rows][cols], and attempt to justify my stand in the following sections.

Tradition: Mathematics and Early Programming Languages

Numerous mathematical operations use vectors and matrices implemented in programs as one- and two-dimensional arrays. Many engineering and scientific disciplines rely on mathematics, including matrix operations.

Tradition may seem like a poor reason for adopting an index order, but I maintain that it is the best and primary reason. Many algorithms, especially for graphics, modeling, and parallel processes, are expressed in mathematical matrix notation. Programmers frequently translate those algorithms into program functions. In my experience, maintaining a consistent notation eases programming, testing, debugging, and documenting. Furthermore, it enhances readability and increases understanding.

Rows First Is "Natural"

Claiming that rows first is "natural" seems subjective and biased. However, two operations reinforce the claim.

#include <iostream>
#include <iomanip>
using namespace std;

int main()
{

    char array[3][2] = { 'A', 'B', 'C', 'D', 'E', 'F' };
    //char array[][2] = { 'A', 'B', 'C', 'D', 'E', 'F' };

    for (int i = 0; i < 3; i++)
    {
        for (int j = 0; j < 2; j++)
            cout << setw(2) << array[i][j];
        cout << endl;
    }

    return 0;
}

#include <iostream>
#include <iomanip>
using namespace std;

int main()
{

    char array[2][3] = { 'A', 'B', 'C', 'D', 'E', 'F' };
    //char array[][3] = { 'A', 'B', 'C', 'D', 'E', 'F' };

    for (int i = 0; i < 3; i++)
    {
        for (int j = 0; j < 2; j++)
            cout << setw(2) << array[i][j];
        cout << endl;
    }

    return 0;
}

 A B
 C D
 E F

 A B
 D E
 ä

Extracting Rows: One Index Access

C++ implicitly implements two-dimensional arrays as one-dimensional arrays of one-dimensional arrays. This organization allows programs to extract and use individual rows, a one-dimensional array, from a two-dimensional array but not individual columns.

#include <iostream>
#include <iomanip>
using namespace std;

void print_row(char* row, int size)
{
    for (int i = 0; i < size; i++)
        cout << setw(2) << row[i];
}

int main()
{
    char array[][3] = {
        'A', 'B', 'C',
        'D', 'E', 'F',
        'G', 'H', 'I',
        'J', 'K', 'L',
    };

    print_row(array[2], sizeof(array[2]) / sizeof(char));

    return 0;
}

#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
    char array[][4] = {
        'A', 'B', 'C', '\0',
        'D', 'E', 'F', '\0',
        'G', 'H', 'I', '\0',
        'J', 'K', 'L', '\0'
    };

    cout << array[2] << endl;

    return 0;
}
 
 
 
 
 
 

 G H I

GHI

Command-Line Arguments

int main(int argc, char* argv[]) int main(int argc, char** argv)
(a)
argv[row][col]
(b)	(c)

Consistency With Java

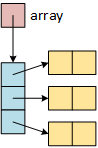
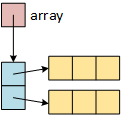
Java is a pure object-oriented language representing fundamental and structured data differently. It represents fundamental data, int, double, etc., as simple bit patterns in memory. In contrast, it represents structured data, including arrays, as objects - instances of an unnamed class.

public int[][] array = new int[3][2];	public int[][] array = new int[2][3];

Index Order Summary

If used consistently, some programs function correctly with either index order. However, some features and the programs utilizing them require a rows x cols or [rows][cols] index order. Other systems require this order, making it customary for C++ programmers. So, throughout this textbook, rows first, followed by columns, is the "correct" order.