9.15.3 Software Development With Objects: The Pouring Puzzle

Time: 00:08:45 | Download: Large, Large (CC), Small | Streaming, Streaming (CC) | Slides (PDF)
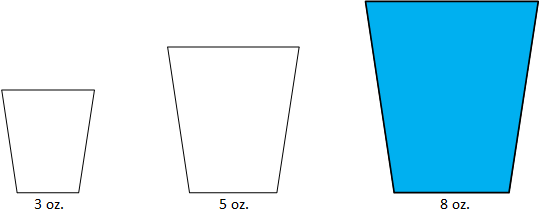
A picture of three glasses of different sizes: 3 ounces, 5 ounces, and 8 ounces. The 8-ounce glass is full; the other two glasses are empty.
The Pouring Puzzle. Three unmarked glasses of different volumes or sizes, 3 ounces, 5 ounces, and 8 ounces, sit on a table. The first two glasses are empty, while the third glass is full of water. The puzzle is how to get at least one glass to hold 4 ounces of water by pouring water from one glass to another (assuming no spillage).

The glasses are unmarked; otherwise, it would be easy to pour water from the large, full glass into the medium-sized glass (i.e., the 5-ounce glass) until it contained 4 ounces (which would also leave 4 ounces in the large glass). So, the only way to "measure" the water is to fill the smaller glasses full.

Our overall problem is to write a program that simulates a person pouring water from one glass to another while attempting to solve the puzzle. We take the common approach of breaking the overall problem down into a series of smaller steps. The first step is to find a suitable representation for the puzzle problem.

Step 1: Representing The Problem

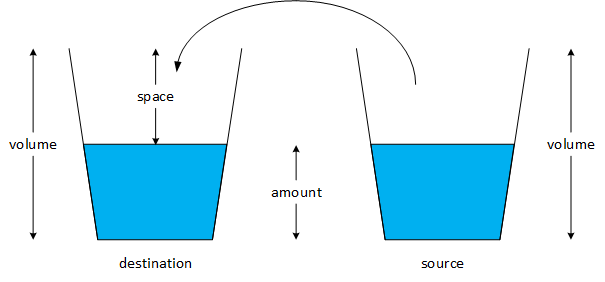
Pictures help us organize the problem's data and identify the missing information. They also make it easier to see the relations between the different parts of the problem. They needn't be "pretty," accurate, or drawn to scale. Although drawing representations of specific situations occurring within a problem might be beneficial, a picture representing a general situation or condition is frequently more helpful. To that end, we begin by drawing a picture of two arbitrary glasses that does not distinguish between the three different-sized glasses and labeling the various parts of the problem. The following figure generally represents any two glasses joined by the pouring process.

A picture of two glass labeled 'destination' and 'source.' Users pour water from the source glass to the destination to solve the puzzle. Three quantities describe both glasses: 'volume is the total amount of water the glass can hold. 'amount' is how much water the glass currently contains. And 'space' is the difference between the 'volume' and the 'amount'.
The roles and attributes of glasses in the pouring puzzle. Drawing a picture to represent a problem is a common first step to solving that problem. Rather than depicting specific glasses, we generalize the representation to two of the three glasses. At any step in the puzzle solution, a glass may play the role of the destination glass, or it may play the role of the source glass. Its position in the pour operation determines a glass's role:

destination.pour(source);

The glass playing the "destination" role can also be called "this" glass. The direction in which we pour the water is quite arbitrary, and we could redefine the pour function so that the "destination" class becomes the function argument and the "source" glass becomes "this" glass. Every glass has two attributes that fully describe or characterize it:

  1. volume: is a glass's size or the maximum amount of water it can hold. Creating a class fixes its volume (i.e., its volume can't change)
  2. amount: is the amount of water currently in the glass; the amount of water changes each time water is poured into or out of the glass

There is also some empty space at the top of a glass when the glass is not full. We could also make space a class attribute, but the program can quickly calculate the value when needed. Furthermore, if we make space an attribute, we must be careful to update it whenever the pour operation changes it. The picture makes the relationship between the three values quite clear: space = volume - amount

The next step is to solve the problem abstractly and develop an algorithm suitable for programming.

Step 2: Object-Oriented Analysis (OOA)

Previously, we examined three phases that are commonly included in software engineering processes: analysis, design, and implementation. As we analyze the pouring puzzle, we note that the problem centers around three objects: a 3-ounce glass, a 5-ounce glass, and an 8-ounce glass. All three glasses have the same attributes: volume and the amount of water currently in the glass.

All three glasses are similar because they represent the same kind of "thing" and have identical attributes. The volume differentiates one glass object from the others. Therefore, we can abstract or generalize the three glass objects into a single Glass class.

In practice, classes described by a UML class diagram are language-independent. We can translate a UML class to Java, C#, or any object-oriented programming language as easily as we can to C++. It is the task of the programmer to add any needed language-specific detail. But as we are still learning the subtleties of C++, two slightly different versions of the Glass class are presented. The only difference between the two versions is the pour function argument (i.e., the argument appearing inside the parentheses).

First version of the Glass UML diagram: Glass ----------------------- -pours : int [underlined] -volume : int -amount : int ----------------------- +Glass(a_volume : int, a_amount : int) +getVolume() : int +getAmount() : int +display() : void +getPours() : int [underlined] +pour(source : Glass&) : void Second version of the Glass UML diagram: Glass ----------------------- -pours : int [underlined] -volume : int -amount : int ----------------------- +Glass(a_volume : int, a_amount : int) +getVolume() : int +getAmount() : int +display() : void +getPours() : int [underlined] +pour(source : Glass*) : void
Pass-by-referencePass-by-pointer
Glass UML class diagram. The underlined features belong to the Glass class as a whole rather than to individual instances of the class (i.e., rather than to individual Glass objects). Class features are implemented by adding the "static" keyword to their definition.

The pour operation changes the amount of water in the destination and source glasses, which it can only do if the program passes the objects by pointer or reference. (Please see Function Argument Passing Summary.) The destination or implicit object is bound to the pour function through the this pointer, which means that it is always passed-by-pointer. But we must choose how to pass the source or explicit object. The way that we pass the explicit argument to the pour function is the only difference between the two UML diagrams. We generally don't show such implementation details on UML diagrams, which are language-independent. I've included the passing notation in the diagrams to help prepare us for the two solutions presented in the following sections.

Step 3: How Much Water To Pour?

A program is just an expression of an existing solution or algorithm. It's okay to write bits of code to test the various steps in a solution, but writing code without having a starting and ending point, and some idea of the path between the two, is slow, frustrating, and not very productive. We begin developing the problem solution by noting that the relation between the space in the destination class and the amount of water in the source glass determines how much water the pour operation can transfer from one glass into the other. There are two cases to consider:

  1. If the remaining space in the destination glass is less than the amount of water in the source glass, then the space in the destination glass determines the amount of water poured from one glass to the other. We can not add more water to a glass than it can hold.
  2. If the remaining space in the destination glass is greater than the amount of water left in the source glass, then the amount of water in the source glass determines the amount of water poured from one glass to the other. We can not pour more water out of a glass than it contains.

Greeno, Collins, & Resnick (1996) report that "Research comparing excellent adult learners with less capable ones ... [confirms] that the most successful learners elaborate what they read" (p. 19). Previously, I suggested that for computer programming students, one of the elaborating steps is asking ourselves if there is more than one way to write the code that solves a problem. The following figure illustrates three different ways of writing code to express the solution developed from the two cases above. How we choose to look at a problem affects our solution. The three code fragments represent the same algorithm viewed from slightly different perspectives.

int	space = volume - amount;

if (space < source.amount)
{
	source.amount -= space;
	amount = volume;
}
else
{
	amount += source.amount;
	source.amount = 0;
}
(a)
int	space = volume - amount;
int	transfer = (space < source.amount) ? space : source.amount;

amount += transfer;
source.amount -= transfer;
(b)
int	space = volume - amount;
int	transfer = min(space, source.amount);

amount += transfer;
source.amount -= transfer;
(c)
Calculating how much water to pour.
  1. A direct statement of the case analysis. If the space in the destination glass equals the amount in the source glass, then both branches of the if-statement yield the same results.
  2. The same algorithm is expressed with a conditional operator, which takes the place of the if-statement and calculates the amount of water to transfer or pour. The amount in the destination glass increase by the amount transferred from the destination glass. The amount in the source glass decreases by the same amount.
  3. We can summarize the two cases above by saying that the amount of water transferred or poured from the source glass to the destination glass is the smallest or minimum of the space in the destination and the amount in the source, which we find with the min function. This solution is compact but requires including an additional header file: <algorithm>.

Step 4: How To Manage The Glasses?

We can create a class named Glass that defines a pour function. We can create a pouring-puzzle program using three instances of the Glass class.

Glass g1;
Glass g2;
Glass g3;
 
destination.pour(source);
 
g1.pour(g2);
g2.pour(g1);
g1.pour(g3);
g3.pour(g1);
g2.pour(g3);
g3.pour(g2);
(a)(b)(c)
Glass objects and their interactions.
  1. Pseudo code for instantiating three Glass objects
  2. source and destination are two instances of the Glass class. The program determines the role an object plays, destination or source, by where it appears in the function call
  3. Any pair of Glass objects can cooperate in the pouring operation. Either object may play the role of the destination or the source glass, depending on which way the puzzle solver wishes to pour water during that move. Six combinations of pouring from one glass to another are possible
if (destination == 1 && source == 2)
	g1.pour(g2);
else if (destination == 2 && source == 1)
	g2.pour(g1);
		.
		.
		.
Selection logic with six separate variables. In this code fragment, source and destination are integers that represent the two glasses that the player has selected for the next pour operation, and an if-else ladder interprets the player's choices. Each possible combination of Glass object interactions - (c) above - is represented by one ladder "rung" or one branch of the if-else ladder. This approach is awkward and error-prone.

A more elegant, more compact, and more easily programmed solution is desirable.

Glass	glasses[3];

while (the puzzle is not solved)
{
	int	source = user input;
	int	destination = user input;
		.
		.
		.
	glasses[destination].pour(glasses[source]);
}
A more elegant solution based on an array of Glass objects. As before, source and destination are integers representing the two glasses the player selected for the next pour operation. The pseudo-code illustrated in the figure still oversimplifies the definition of the array and the instantiation of the three Glass objects. Nevertheless, the highlighted code demonstrates how an array elegantly collapses the if-else ladder.
Array definitionPassing the source glass
by referenceby pointer
Glass glasses[3]...;glasses[d].pour(glasses[s]);glasses[d].pour(&glasses[s]);
Glass* glasses[]...;glasses[d]->pour(*glasses[s]);glasses[d]->pour(glasses[s]);
Defining the glasses array and calling the pour function. We can make the array on the stack as an array of objects, or we can make it on the heap as an array of pointers. Regardless of where we make the array, we can choose which passing technique we want by selecting the appropriate operators. To make the summary table easier to display, we allow d and s to represent indexes selecting the destination and source glasses, respectively; we also defer the detail represented by the ellipses to the following sections.

Step 5: The Puzzle Logic

Roughly outlining the overall program logic is the final step before programming, which we do with the following logic diagram.

A logic diagram of the puzzle logic. The logic begins with a test: if glass2.amount != 4 and glass3.amount != 4. If the test is false (at least one of the glasses contains exactly four ounces), the program prints a winning message, the final amounts, and the total number of pours. But if the test is true, none of the glasses contain exactly 4 ounces, then the following sequence of operations is performed. Print the amount and volume of all three glasses. Prompt for and read destination glass. Prompt for and read source glass. Pour from source to destination. Then the program returns to the test to determine if any glass contains exactly 4 ounces.
A logic diagram describing a framework for solving the pouring puzzle problem. The diamond at the top of the diagram represents a test. If the test is true, the arrows form a loop. This observation suggests that much of the puzzle logic will reside inside the body of a looping control statement. If g1 represents the 3-oz. glass, we can eliminate it from the test because it can never contain 4 ounces.

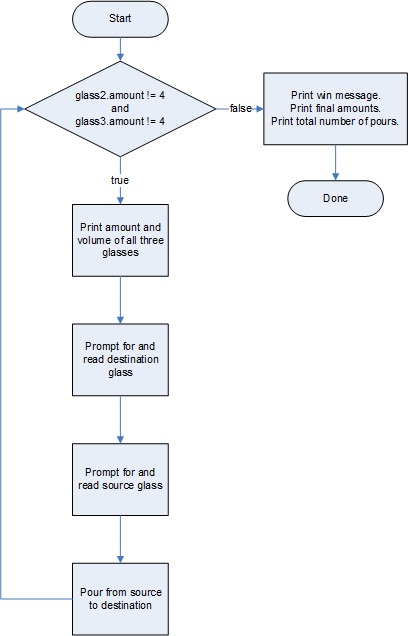
Two similar program versions are developed in the following sections. The first program creates an automatic array of Glass objects on the stack. The second program creates a dynamic array on the heap with the new operator.