7.13. Dynamic And Multi-Dimensional Arrays

Time: 00:06:00 | Download: Large, Large (CC), Small | Streaming, Streaming (CC) | Slides (PDF)
Review

C++ doesn't limit the number of array dimensions programs can create and use. Creating arrays with two or more dimensions as automatic or local variables on the stack is straightforward. However, it is surprisingly more difficult to create them dynamically on the heap with the new operator. Some seemingly natural ways of dynamic array allocation do not work.

Dimensions Automatic (Local, Stack) Dynamic (Heap)
1 
int scores[15];
 
int* scores = new int[15];
 (a)(b)
2 
int scores[15][10];
 
int* scores = new int[15][10];		// (1)
int** scores = new int[15][10];		// (2)
int* scores[50] = new int[15][10];	// (3)
 (c)(d) - Syntax Errors
2   
int** scores = new int* [nrows] { new int[ncols] };
int** scores = (int **) new int[nrows][ncols];
int** scores = reinterpret_cast<int **>(new int[nrows][ncols]);
  (e) - Runtime Errors
Automatic vs. dynamic array allocation. Programs must specify the size of each dimension with a compile-time constant when creating an array automatically on the stack. However, they can use variables when creating them dynamically on the heap. The benefits of this flexibility motivate our exploration of dynamic multi-dimensional array syntax.
  1. The syntax for creating a one-dimensional array automatically as a local or stack variable.
  2. The syntax for creating a one-dimensional array dynamically with the new operator as a heap variable.
  3. The syntax for creating a two-dimensional array automatically as a local or stack variable.
  4. Incorrect statements failing to create a dynamic two-dimensional array.
    1. The new operator returns a single pointer, seemingly justifying defining scores as a single-dimensional pointer variable, but compilation fails with the diagnostic: "cannot convert from 'int (*)[10]' to 'int *'."
    2. The diagnostic suggests that scores is an integer pointer, but compiling the modified statement fails with a similar diagnostic: "cannot convert from 'int (*)[10]' to 'int **'."
    3. The final version also fails with: "cannot convert from 'int (*)[10]' to 'int *[10]'."
  5. Programmers can force the dynamic allocation operations to compile with "creative" initialization syntax (the first statement) or typecasts (the second and third statements), only to see them fail with runtime errors.

The failures of (d) and (e) notwithstanding, programs can create multi-dimensional arrays dynamically. The following discussion presents three solutions:

Automatic Type Deduction

The ANSI standard's 2011 extension of the auto keyword affords a partial solution for the multi-dimensional dynamic array problem. While the solution is limited, its simplicity makes it the favored approach, if the program can function within the limitation.

#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
	int nrows = 15;
	const int ncols = 10;

	auto scores = new int[nrows][ncols];

	for (int i = 0; i < nrows; i++)
		for (int j = 0; j < ncols; j++)
			scores[i][j] = i * j;

	for (int i = 0; i < nrows; i++)
	{
		for (int j = 0; j < ncols; j++)
			cout << setw(5) << scores[i][j];
		cout << endl;
	}

	return 0;
}
auto detecting a two-dimensional array type. The compiler can automatically detect a variable's type by using the auto keyword, circumventing the need for a programmer to determine the appropriate type. This technique resolves some of the problems presented in Figure 1 (d) and (e). The solution allows programmers to use a variable for the first array dimension but still requires compile-time constants for the second and subsequent dimensions.

Creating Two-Dimensional Arrays As An Array Of Arrays

Java takes a different approach to creating multi-dimensional arrays: it creates arrays of arrays. Specifically, creating a two-dimensional array begins by creating a one-dimensional array whose elements are one-dimensional arrays. C++ programs can take the same approach with two advantages: Programmers can specify each dimension size with a variable (rather than a compile-time constant), and the indexing or element access notation is straightforward. However, it has two disadvantages: Creating the arrays is a complex, multi-step process, and the program must deallocate the arrays to avoid a memory leak.

The textbook first introduced arrays-of-arrays as a way to return two-dimensional arrays from functions with the return operator. But programmers can also use this "trick" to create multi-dimensional arrays dynamically with new. Only the last dimension's array saves data when extended to three and higher dimensions, while the other dimensional arrays contain pointers. The advantages and disadvantages continue in higher dimensions, but the disadvantages become more pronounced with each additional dimension.

The picture consists of a pointer variable named 'table,' a vertical array with 'nrows' elements, and several horizontal arrays denoting rows, each with 'ncols' elements. An arrow points from 'table' to the vertical array, and each element of the vertical array points to a row. 
#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
    int    nrows;
    int    ncols;

    cout << "Number of rows: ";
    cin >> nrows;
    cout << "Number of columns: ";
    cin >> ncols;

    int**    table = new int* [nrows];		  // (1)

    for (int i = 0; i < nrows; i++)		  // (2)
        table[i] = new int[ncols];

    for (int row = 1; row <= nrows; row++)
        for (int col = 1; col <= ncols; col++)
            table[row-1][col-1] = row * col;	  // (3)

    for (int row = 0; row < nrows; row++)
    {
        for (int col = 0; col < ncols; col++)
            cout << setw(4) << table[row][col];   // (3)
        cout << endl;
    }
    
    for (int i = 0; i < nrows; i++)		  // (4)
        delete[] table[i];
    delete[] table;

    return 0;
}
(a)(b)
The multtab example implemented as an array of arrays.
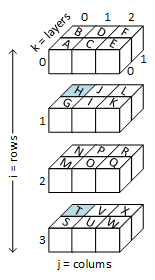
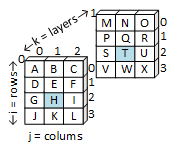
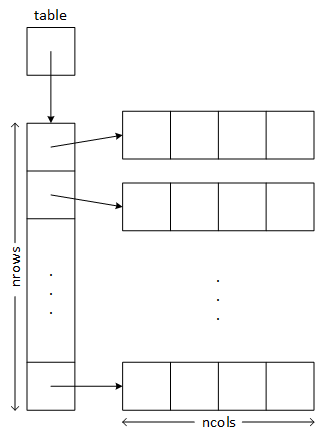
  1. table is a pointer to a pointer (i.e., it's a pointer with two levels of indirection as illustrated in b.1). table points to an array of row pointers. Each row pointer points to an array that serves as one table row.
    1. The program defines table as int**, meaning that it is a pointer to a pointer. The data type int* means that each element of table is a pointer to an integer, that is, an array of integers.
    2. The program must create each row of the table one at a time.
    3. One of the advantages of creating a two-dimensional array as an array or arrays is that the "client" or main-logic code can continue to use the two-index notation: table[row][col].
    4. The program must individually delete the rows and then the array of pointers. The square brackets, [], informs delete it is operating on an array.

Extending Row-Major Ordering To Three Dimensions

The following discussion extends to three dimensions ideas first introduced in the context of two-dimensional arrays:

In the case of three-dimensional arrays, the "natural" initialization order and rows×columns×layers view are not the same. The difference forces programmers to choose which view most closely matches a given problem or is the easiest to program. While they can create different row-major ordering operations for each view, the operations may not always follow the general formula.

Example Program Initialization Order Console Output 
#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
    char  array[4][3][2] = {
        'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L',
        'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X' };

    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 3; j++)
        {
            for (int k = 0; k < 2; k++)
                 cout << setw(2) << array[i][j][k];
            cout << endl;
        }

    return 0;
}
 A picture showing four stacked layers. Each layer is three elements wide by two elements deep. Reading left to right, front to back, the top layer (corresponding to i = 0) has the characters A, B, C, D, E, and F. The next layer (i = 1) has G, H, I, J, K, and L in the same reading order. This pattern continues, filling the next two layers (i = 2 and i = 3). The letters H and T are shaded in blue to help locate them in the row-major function example. 
 A B
 C D
 E F
 G H
 I J
 K L
 M N
 O P
 Q R
 S T
 U V
 W X
(a)(b)(c)
3D array: initialization order. When a program uses a linear initializer list to fill a three-dimensional array, the list fills the array from the rightmost dimension, making those elements contiguous in memory.
  1. The program fills a three-dimensional array with letters and displays them on the console with three nested for-loops.
  2. An abstract representation of a three-dimensional array's elements as filled by the example's initializer list.
  3. The program's output.
Three-dimensional arrays are more common in mathematically-intensive domains (e.g., simulations, modeling, graphics, etc.) than general programming. Less common still is the need to initialize them with an initializer list of values known when programmers write the code.
Example Program Console Output 
#include <iostream>
#include <iomanip>
using namespace std;

inline int index(int i, int j, int k, int ncols, int nlayr) { return k + nlayr * (j + ncols * i); }

int main()
{
    int nrows = 4;
    int ncols = 3;
    int nlayr = 2;

    char*  array = new char[nrows * ncols * nlayr] {
        'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L',
        'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X' };

    cout << index(1, 0, 1, ncols, nlayr) << " -> " << array[index(1, 0, 1, ncols, nlayr)] << endl;
    cout << index(3, 0, 1, ncols, nlayr) << " -> " << array[index(3, 0, 1, ncols, nlayr)] << endl;

    return 0;
}
 
7 -> H
19 -> T
Dynamic 3D array and row-major ordering. The order an initializer list fills an array is independent of where the array's memory is allocated (stack or heap). The program creates a three-dimensional array dynamically on the heap with the new operator. Although Figure 1 demonstrates that new fails when creating multi-dimensional arrays, this example succeeds by synthesizing multiple dimensions from a single dimension (blue) and a row-major indexing function (pink). The program calls the indexing function to access a specific array element, mapping from the problem's three dimensions (specified by i, j, and k) to the array's linear single dimension (gold).

Specifying the size of each dimension with a variable allows programs to read or calculate the sizes while they run. The program implements the indexing function, index, as an inline function function for efficiency. It doesn't depend on the number of rows but requires the number of columns and layers. So, function calls require five arguments, making them somewhat cumbersome but also making them flexible - it works with any three-dimensional array. The cout statements locate the elements representing H and T (shaded in blue in the previous figure) using the ordering function.

Row × Column × Layer Order

Typically, programs solving problems with three-dimensional arrays read or calculate the values saved in each array element rather than taking them from an initializer list. This situation allows programmers to choose a mental or abstract array view different from the initializer list storage order. The following examples use a series of assignment operations, three per line for compactness and to match the row-first storage order, but would be part of the problem solution in a more authentic program.

Example Program Rows×Cols×Layers Console Output 
#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
    char  [4][3][2];
    array[0][0][0] = 'A'; array[0][1][0] = 'B'; array[0][2][0] = 'C';
    array[1][0][0] = 'D'; array[1][1][0] = 'E'; array[1][2][0] = 'F';
    array[2][0][0] = 'G'; array[2][1][0] = 'H'; array[2][2][0] = 'I';
    array[3][0][0] = 'J'; array[3][1][0] = 'K'; array[3][2][0] = 'L';
    array[0][0][1] = 'M'; array[0][1][1] = 'N'; array[0][2][1] = 'O';
    array[1][0][1] = 'P'; array[1][1][1] = 'Q'; array[1][2][1] = 'R';
    array[2][0][1] = 'S'; array[2][1][1] = 'T'; array[2][2][1] = 'U';
    array[3][0][1] = 'V'; array[3][1][1] = 'W'; array[3][2][1] = 'X';

    for (int k = 0; k < 2; k++)
        for (int i = 0; i < 4; i++)
        {
            for (int j = 0; j < 3; j++)
                cout << setw(2) << array[i][j][k];
            cout << endl;
        }

    return 0;
}
 A picture showing a 4 by 3 by 2 box sliced front to back into two layers. Each layer has four rows (top to bottom) and three columns (left to right). Reading left to right, top to bottom, the from layer or face has the letters A B C (top row, i = 0), D E F (second row, i = 1), G H I (third row, i = 2), and J K L (bottom row, i = 3). The back layer continues the pattern with the letters M through X. The letters H and T are shaded in blue to help locate them in the row-major function example. 
 A B C
 D E F
 G H I
 J K L
 M N O
 P Q R
 S T U
 V W X
(a)(b)(c)
3D array: row × column × layer order. The program demonstrates a three-dimensional array following my preferred rows×columns×layers view. I find this view easier to visualize and program than the initializer list notation, but the program must explicitly save the initial values in each element.
  1. Programmers must know the size of each dimension and specify them with compile-time constants (blue) when they write the program. The program tediously saves the initial value of each array element, but "real" programs subsume this step in the data input and problem calculations. The program alters the "normal" for-loop execution order (the k-loop is on the outside) to achieve the desired array output.
  2. An abstract representation illustrating a three-dimensional array in memory with the letters 'A' through 'X' saved in row×column×layer order.
  3. The program's output corresponds to my preferred view.
Example Program Console Output 
#include <iostream>
#include <iomanip>
using namespace std;

inline int index(int i, int j, int k, int nrows, int ncols) { return nrows * ncols * k + (j + ncols * i); }

int main()
{
    int nrows = 4;
    int ncols = 3;
    int nlayr = 2;

    char*  array = new char[nrows * ncols * nlayr] {
        'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L',
        'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X' };

    cout << index(2, 1, 0, nrows, ncols) << " -> " << array[index(2, 1, 0, nrows, ncols)] << endl;
    cout << index(2, 1, 1, nrows, ncols) << " -> " << array[index(2, 1, 1, nrows, ncols)] << endl;

    return 0;
}
 
7 -> H
19 -> T
3D array: row × column × layer indexing. The program creates a three-dimensional array dynamically on the heap with new. This technique allows programmers to specify the number of dimensions and sizes with runtime variables (blue). The cost of these benefits is they must synthesize three dimensions from one with an indexing function (pink). Although based on the row-major ordering, the function does not follow the general formula: it requires the number of rows and columns. To locate an element in layer k, it must skip all elements in the layers <k, calculated by nrows*ncols*k.
Developing the indexing functions is a challenging task. Nevertheless, the functions are good examples of nuts and bolts programming. Completing these programming tasks is a three-step process. First, find a suitable abstract problem representation. Pictures are often a useful way to represent a problem. They help me visualize, identify, and organize relationships and other problem information. Pictures form a bridge to the second and most challenging step of developing the algorithms for solving the current problem. Programming problems consist of a sequence of story problems, and programs consist of algorithms solving those problems. The final step translates the pictures and algorithms into working code. Each step, especially the second, requires frequent practice.